Research

My research focuses of Core-Collapse Supernovae,
Nuclear Equation of State, Neutrino Physics and more...

Background

The physics of Supernovae

A Core-Collapse Supernova (CCSN) is an extremely energetic explosion that happens at the end of the life of a massive star. It is effectively the death of a star. If you want to know more about Supernovae, I have an awesome website for you. Trust me, it's great! If you're looking for an educational video, this one is extremely well-made. For a more technical discussion, see either Review 1 or Review 2

The computational aspect of Supernovae

CCSNe are extremely complicated environments since they are affected by forces that act on macroscopic scales (like gravity) and forces that act on microscopic scales (like the electroweak force and the strong force). To understand the physics behind supernovae, one has to unquestionably rely on numerical simulations. But that's not the end of the story! If you want to reliably simulate an explosion, you need to use some of the most powerful supercomputers available. Once you have access to them, it still takes millions of CPU hours to do it! An alternative is to simplify the problem (which is pretty much 99% of what Physicists do) and, for example, pretend that the star is perfectly spherically symmetric. That's what I do, and it might be surprising, but simply by doing that, one cuts down the cost of a simulation to hours rather than millions of hours. Keep scrolling if you want to know all the cool things that can be done even with such a simplified model!

The role of neutrino-driven turbulent convection in CCSNe

Neutrino-driven turbulent convection is widely considered one of the main (if not the main) mechanisms that enable shock revival in supernovae, as many 3D simulations have shown. A fraction of the neutrinos produced in the proto-neutron star interacts with the material behind the shock (in the so-called gain region), and increases its entropy. This creates a negative entropy gradient, which triggers turbulent convection. The convective blobs can then transfer the energy to the shock, hence enabling the explosion. In my research, I use a spherically-symmetric, open-source code called GR1D to simulate the collapse of massive stars and subsequent shock revival. However, by imposing spherical symmetry, one loses all the information about non-radial motions, such as turbulence. Luckily, some parametric models can take the energy transfer due to turbulent convection into account. We modified one of these models (called STIR) to take general relativistic effects into account (and we wrote this paper about it!).
In the following video you can see the collapse of a 20 solar mass star and subsequent shock revival. A more detailed description is given below.

The expanding solid line shows the location of the shock, the dashed line shows the outer edge of the Proto-Neutron Star and the dashed-dotted line shows the location of the gain radius. Remember, the gain region is the region between the gain radius and the shock!. The color scale for the leftmost panel shows the entropy in the star, while the one for the rightmost panel shows the Brunt–Väisälä frequency, which tells you where convection can develop (red regions) or cannot develop (blue regions). The most interesting panel is the middle one, where the color scale shows the magnitude of the turbulent velocity generated in our model, both in the gain region and deep inside the PNS. Normally, with the model described in the aforementioned paper, you would see no turbulent velocity inside the PNS. However, by tuning the parameters that control the amount of turbulent convection in the PNS, one can obtain turbulent velocities like the ones shown in the movie, which agree quite well with the 3D results. We are still working on this, so stay tuned!

The role of the Si/O interface in the explodability of CCSNe

Simulations of core-collapse supernovae start when the iron core of the star is unstable, and therefore it collapses. One must therefore model the evolution of the star from its birth up to when it starts collapsing. This is usually done using a stellar evolution code. The supernova simulation then picks up when the stellar evolution code stops. In this paper I analyzed the impact of using pre-collapse models from two different stellar evolution codes: KEPLER and FRANEC. Usually, in the supernova community most groups almost always use KEPLER progenitors, because historically they were the first models comoputed. However, I showed that using progenitors from different stellar evolution codes can massively change the results.

Above you can see how the explodability pattern depends on the initial mass of the star at birth (the ZAMS mass). You can see that there are bands for different values of &alpha. They basically represent how strong neutrino-driven convection is, but don't worry too much about it, just focus on &alpha=1.51. Green corresponds to explosions and blue corresponds to failed supernovae. You can see how the low-mass FRANEC models explode more readily than the KEPLER models, whereas around 22 solar masses KEPLER progenitors explode whereas FRANEC progenitors don't. Therefore, the supernova community should soon start analyzing the effects of changing the input models of their calculations, because they clearly have a huge effect of the explosion. In this same paper I also developed a criterion that predicts whether a star explodes based on its density profile right before it collapses. It's pretty cool because it's a relatively simple model, and it tells you if your star is gonna blow up or not without the need of doing the simulation. It's not perfect of course, but the accuracy is around 90%, which is very good for such a simple model! The idea is that near the silicon-oxygen interface there is a big density drop. When this is accreted through the shock, suddenly the density goes down, and therefore it's easier for the shock to expand, because there's less stuff pushing it down. Combined with neutrino-driven turbulence that pushes the shock from below, sometimes this leads to an explosion, depending how big is the density drop. This is my favorite result so far, because I was able to develop a simple, physically consistent criterion from start to finish. It can be used in population synthesis models, galactic chemical evolution etc... It also has very interesting implications, and shows that including neutrino-driven convection is crucial to obtain the correct explodability. Lastly, it agrees with results obtained by the 2D simulations of the Pronceton group, who indipendently developed a very similar criterion to mine. A natural follow-up would be being able to predict remnant masses and yields, so I'm gonna get to work and try to do that!

The role of the Nuclear Equation of State in CCSNe

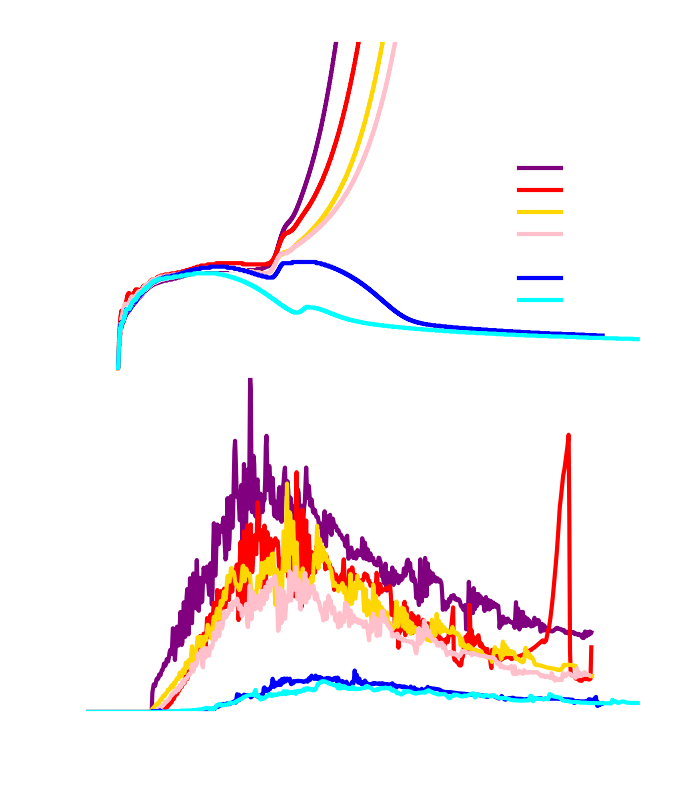
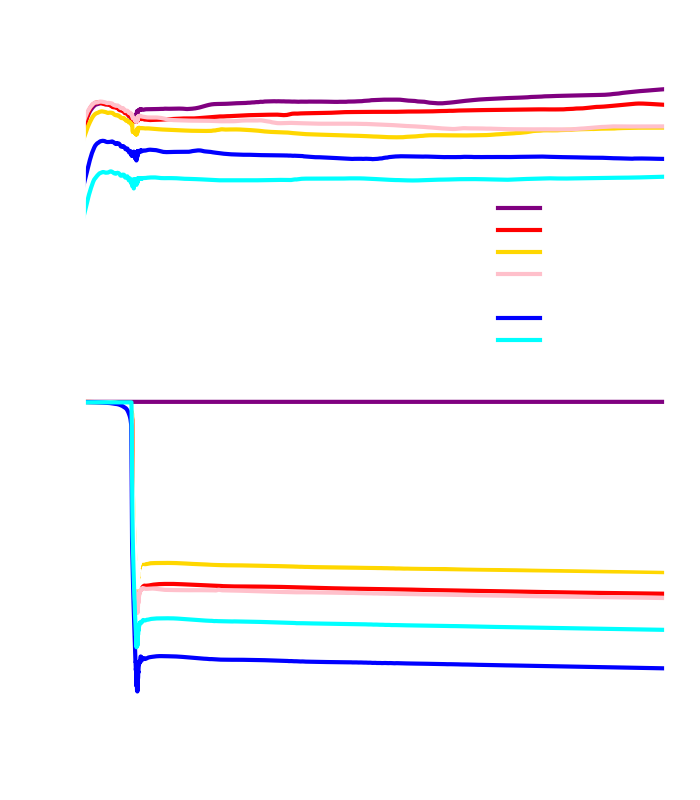
CCSNe are heavily affected by how nuclear matter - that is, matter stripped down to its fundamental constituents - behaves under the extreme conditions reached during the explosion. The general idea is that when a star runs out of fuel and suddenly collapses, matter will be squeezed together and heated up. The detailed model describing how quickly this ball of material heats up and how dense it can become is called the Equation Of State (EOS) of nuclear matter. In a simplified scenario, one can imagine that if matter does not heat up very much and becomes too dense, it will not generate enough "steam" to power an explosion. Therefore, depending on the equation of state, one might get a stronger or weaker explosion or no explosion at all.

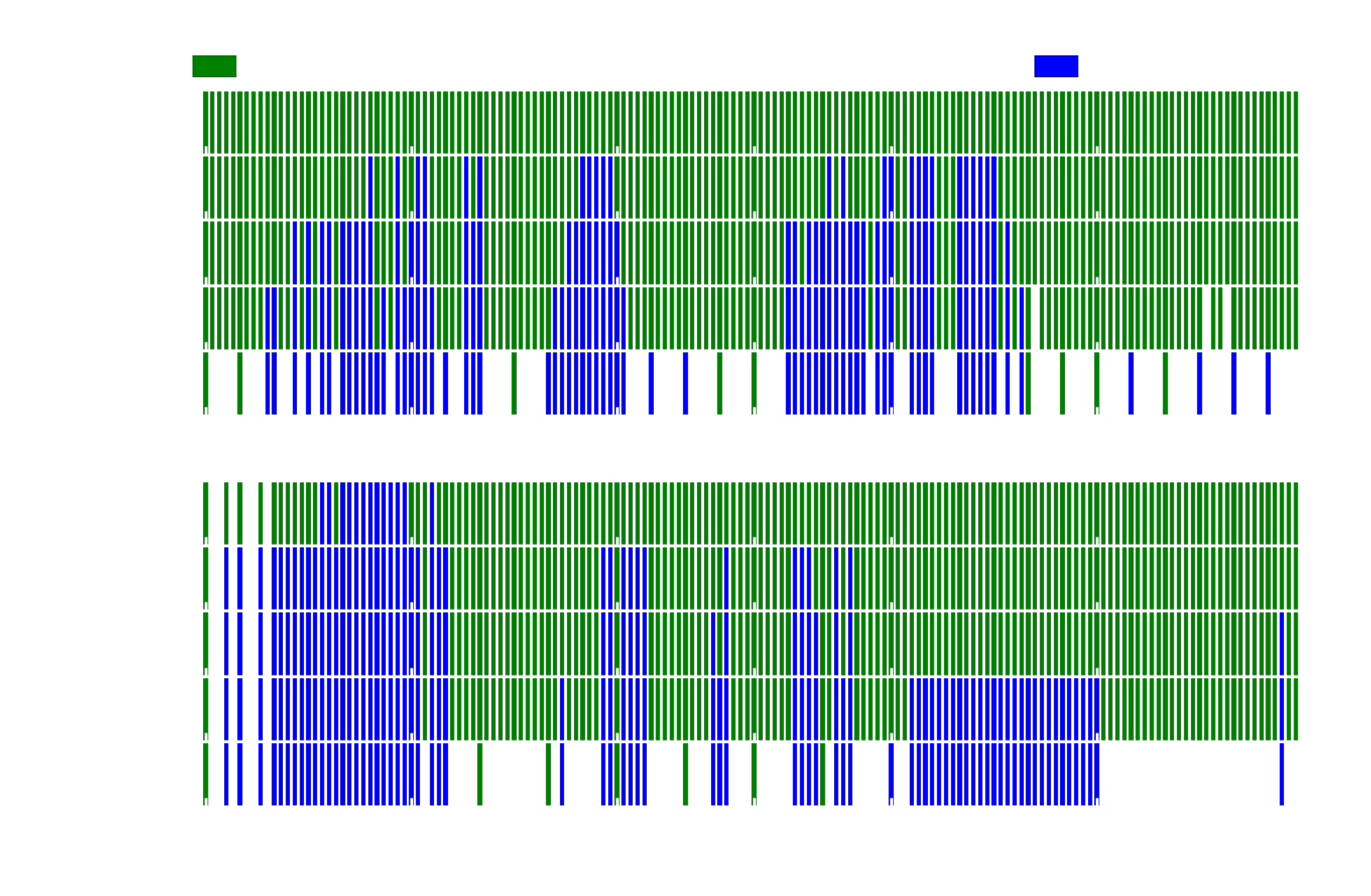
On the top left, you can see the shock radius vs time after bounce. On the bottom left E_PNS represents the energy of convection inside the Proto-Neutron Star. On the right, one can see the central entropy and the effective nucleon mass in the first 50 milliseconds after bounce. Different colors correspond to different EOSs. As you can see, there is a strong correlation between the strength of explosion and central entropy, which is also reflected in E_PNS. On the contrary, there is no correlation with effective nucleon mass, seen in previous works. If you want to know more about this, read my paper)!

The role of General Relativity in CCSNe

General Relativity is known to be a very important theory when it comes to describing very dense astronomical objects. However, for a "lighter" object like the Sun, one finds no difference between describing it using General Relativity (GR) or the good old Newtonian theory of gravity. Supernovae are somewhere in between. Densities at the very center of the newly formed Proto-Neutron Star are indeed large enough to require a general relativistic description, but for now, most simulations have been carried out with a modified Newtonian potential, which is close to GR but is not quite the same as a full GR formulation. We decided to investigate how different is the impact of turbulent convection on the explosion if one uses Newtonian gravity vs. GR. In particular, since GR can change the structure of the stars (making them more or less compact), we wanted to see if it affects stars of different masses in the same way. To do that, we used the code described above to run GR and Newtonian simulations of different progenitors, and see which ones explode and which ones don't. The main Figure of our paper is described below.

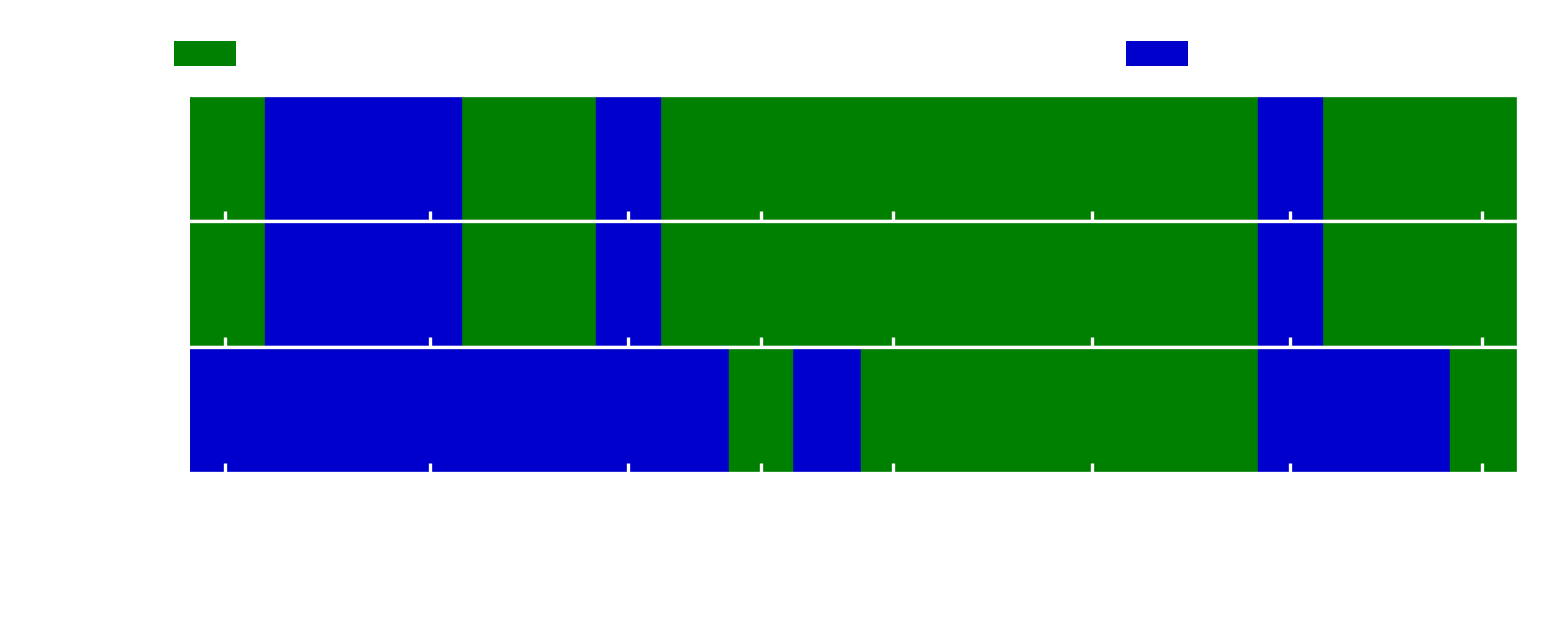
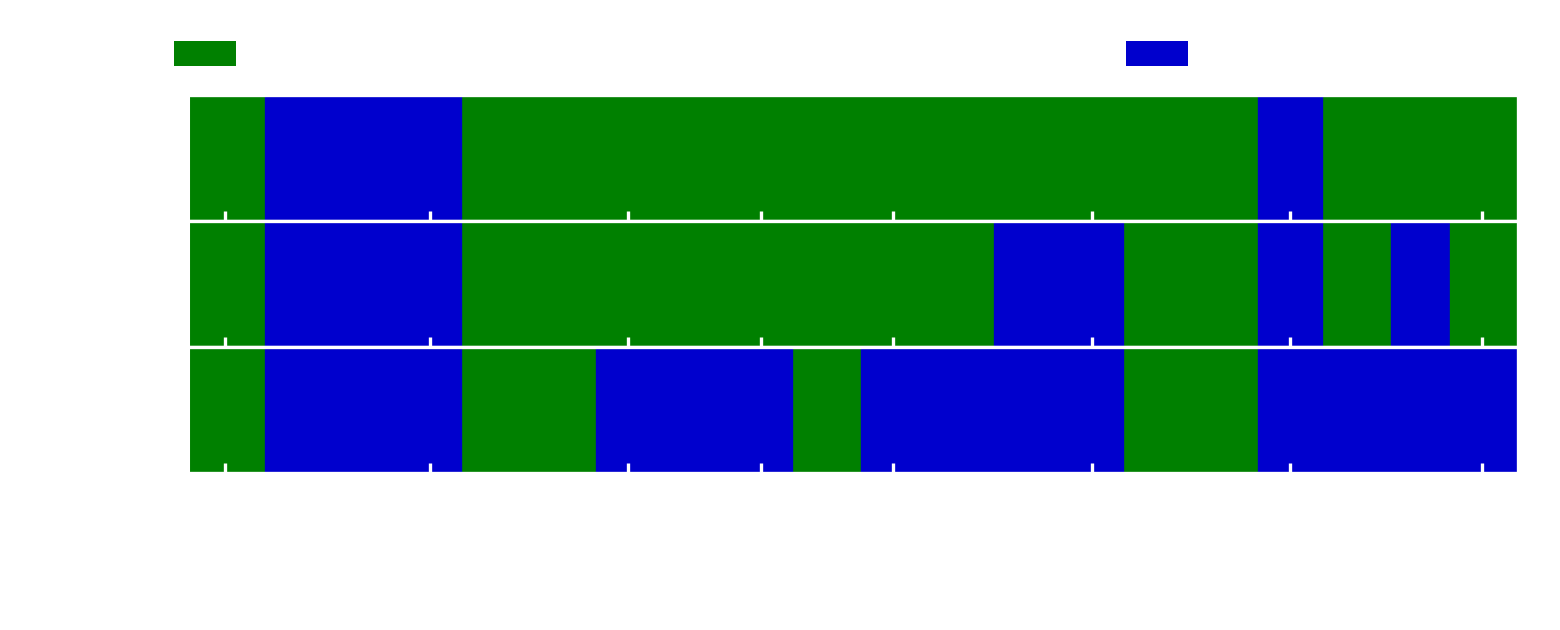
This Figure shows how different progenitors explode with and without GR. The parameter on the y-axis controls how strong the convection is (don't worry too much about it, but if you really want to you can read our paper). As you can see, in the middle panels the patterns look quite different if you compare GR and GREP (which stands for General Relativistic Effective Potential, and it's basically the modified Newtonian approach that I was describing above).
The main conclusion one can draw from this Figure is that General Relativity might change which stars explode and which ones do not. It should therefore be included in more sophisticated 3D simulations.

Future Work

I want to find a realistic model for PNS convection in spherical symmetry. It requires correctly including the contribution of the lepton fraction gradient in the analysis of the instability, which is not trivial. However, there might be ways to do it, so I am working on taht right now, stay tuned!